Математика - это наука, которая изучает числа, формулы, отношения и многое другое. Однако весь этот мир математических истин нужно строить на основе определений, утверждений и правил. В этом контексте важно различать такие понятия, как лемма, теорема и аксиома. Каждое из этих понятий имеет свою специфику и роль в математике.
Лемма - это простое вспомогательное утверждение, которое помогает доказать более общую теорему. Леммы обычно не являются самостоятельными и не вызывают особого интереса с точки зрения исследования. Они являются посредниками между известными и новыми теоремами, помогая установить связь или обобщить уже имеющиеся результаты.
Примером леммы может служить утверждение о сумме углов треугольника, которое необходимо для доказательства более общей теоремы о сумме углов в многоугольнике.
Теорема - это утверждение, которое было доказано и является фундаментальным для математических наук. Теорема имеет широкое применение и широкий интерес для математиков, а также конкретные условия, при которых она выполняется. Для доказательства теоремы можно использовать леммы, аксиомы и другие уже доказанные теоремы.
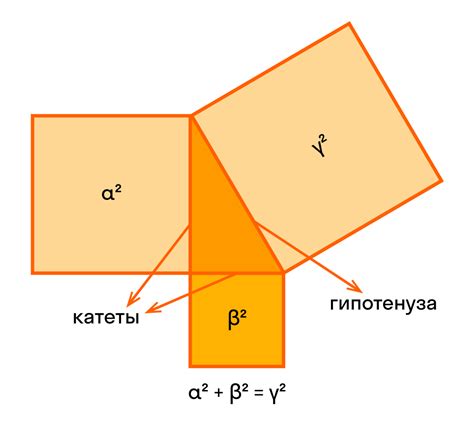
Примером теоремы может служить теорема Пифагора, которая устанавливает связь между длинами сторон прямоугольного треугольника. Эта теорема является одной из базовых основ геометрии и имеет широкое применение в практике.
Аксиома - это неотъемлемое утверждение, которое принимается без доказательства как истинное. Аксиомы представляют собой фундаментальные принципы, на которых строится вся математика. Они задают основные свойства и отношения объектов, такие как числа, пространство и т. д. Аксиомы нельзя вывести из других утверждений, они принимаются как неоспоримые истинности.
Пример аксиомы - аксиома параллельных прямых в евклидовой геометрии, которая утверждает, что через точку, не лежащую на данной прямой, проходит ровно одна прямая, параллельная данной.
Таким образом, леммы, теоремы и аксиомы выполняют разные функции в математике. Леммы являются вспомогательными утверждениями, которые помогают доказывать более общие теоремы, теоремы - фундаментальными утверждениями, которые имеют широкое применение, а аксиомы - неотъемлемыми основами, на которых строится вся математика.
Что такое лемма?

Леммы обычно являются довольно специфичными и узконаправленными утверждениями, связанными с основной теоремой, но несамостоятельными. Они часто формулируются и доказываются перед основной теоремой, чтобы облегчить последующее доказательство. Леммы могут также использоваться для обобщения и уточнения различных деталей в доказательствах.
Для лемм характерно наличие доказательств, которые основываются на уже известных аксиомах, теоремах или других леммах. Обычно леммы не являются самостоятельными достаточными условиями для получения какого-либо утверждения, но служат промежуточными шагами на пути к доказательству.
Что такое теорема?
Теоремы обозначаются обычно буквами латинского алфавита, такими как А, В или С. Контекст и область применения теоремы обычно определяются названием теоремы после ее обозначения. Теоремы могут быть условными или безусловными, в зависимости от того, требуется ли выполнение определенных предположений для применения теоремы.
Теоремы являются одним из важных инструментов математики и играют ключевую роль в развитии новых концепций и теорий. Их доказательства и применения являются основным способом достижения новых открытий и построения математических моделей для решения проблем и задач в науке и практике.
Что такое аксиома?

Аксиомы являются фундаментальными принципами математической теории, которые определяют ее основу и свойства. В отличие от теорем и лемм, аксиомы не нуждаются в доказательстве, так как они принимаются как самоочевидные и истиные.
Аксиомы обычно формулируются в виде логических утверждений или предикатов, которые описывают фундаментальные свойства объектов, на которых строится данная математическая теория. Например, в геометрии одной из аксиом может быть утверждение о том, что через две различные точки можно провести прямую.
Разница между леммой и теоремой

| Лемма | Теорема |
|---|---|
| Это вспомогательное утверждение, которое используется для доказательства более глобальной математической теоремы. | Это основное утверждение, которое может быть доказано математическими методами. |
| Обычно леммы имеют более узкое применение и они используются только в контексте определенной теоремы. | Теоремы имеют более широкое применение и могут быть использованы в различных областях математики. |
| Лемма может быть доказана, используя уже доказанные теоремы или аксиомы. | Теорема должна быть доказана самостоятельно, без использования других утверждений. |
| Лемма обычно имеет более короткое и простое доказательство, чем теорема. | Теорема может иметь более сложное и подробное доказательство. |
Таким образом, лемма и теорема являются важными элементами математического доказательства, но они отличаются друг от друга по своей природе, применению и способу доказательства.
Разница между теоремой и аксиомой
В математике термины "теорема" и "аксиома" имеют существенные различия. Возникает вопрос: чем они отличаются и какая роль каждого понятия в научной деятельности математиков?
Теорема - это утверждение в математике, которое доказано на основе аксиом или других теорем. Теорема обладает высоким уровнем вероятности истины, так как ее доказательство является строгим и непреложным.
Разница между теоремой и аксиомой заключается в их статусе и функциях в математической науке. Теоремы, как уже упоминалось, подтверждаются доказательством и допускают возможность опровержения. Они стремятся к определенной цели - доказать или опровергнуть некоторое математическое утверждение.
Аксиомы, напротив, служат согласованными истинами, на основе которых строится математическая система. Они являются базовыми принципами, которым математики придерживаются при разработке и изучении новых результатов. Аксиомы, в отличие от теорем, не требуют доказательства и считаются незыблемыми истиными положениями.



