В математике существует несколько понятий, связанных с делимостью чисел - это делители и кратные. Часто эти термины путаются и не вполне понятны друг другу. Однако делители и кратные - это два совершенно разных понятия, которые используются в разных контекстах и имеют свои специфические свойства.
Делитель - это число, на которое заданное число делится без остатка. Если число A делится на число B без остатка, то B является делителем числа A. Например, число 10 делится на числа 1, 2, 5 и 10, поэтому эти числа являются делителями числа 10. Делители могут быть как положительными, так и отрицательными. Также делителем может быть ноль, но в этом случае деление на ноль невозможно, поэтому делители должны быть отличными от нуля.
С другой стороны, кратное - это число, которое делится на заданное число без остатка. Если число B делится на число A без остатка, то A является кратным числа B. Например, число 15 кратно числу 5, так как 15 делится на 5 без остатка. Кратным числам также могут быть как положительные, так и отрицательные числа.
В чем разница между делителем и кратным числом в математике?

Число, которое делится на другое число без остатка, является его делителем. То есть, если число а делится на число b без остатка, то b является делителем числа а. Например, делителями числа 10 являются числа 1, 2, 5 и 10.
С другой стороны, кратные числа образуются путем умножения числа на другое число. Кратное число не является делителем самого числа, но может делиться на него без остатка. Например, числа 20, 40, 60 и так далее являются кратными числа 10.
Таким образом, разница между делителем и кратным числом состоит в том, что делитель делится на число без остатка, тогда как кратное число получается умножением числа на другое число.
Определение понятий "делитель" и "кратное число"

Делитель – это число, на которое другое число делится без остатка. Например, числа 2 и 3 являются делителями для числа 6, потому что 6 делится на них без остатка (6 : 2 = 3 и 6 : 3 = 2). В математической записи делителей можно указывать с помощью символа "∣". Так, число 6 можно представить в виде 6 = 2∣6 и 3∣6.
Кратное число – это число, которое делится на другое число без остатка. Например, числа 12, 24 и 36 являются кратными числами для 6, потому что они делятся на 6 без остатка (12 : 6 = 2, 24 : 6 = 4 и 36 : 6 = 6). В математической записи кратных чисел можно указывать с помощью символа "∣". Так, можно сказать, что число 12 является кратным числом для 6, записывая это как 12∣6.
Важно отметить, что число, которое делится без остатка на другое число, всегда является кратным этому числу. То есть, если число а делится на число b без остатка, то число a – это кратное число для b. Однако, не все кратные числа являются делителями для данного числа.
Например, число 6 является делителем для самого себя, а также для чисел 2 и 3. Однако, кратными числами для 6 являются также число 12, 18 и другие, которые делятся на 6 без остатка.
Таким образом, понятия "делитель" и "кратное число" в математике тесно связаны с делением и являются основными для исследования числовых значений и их свойств.
Делитель: свойства и характеристики
Вот основные свойства и характеристики делителей:
| Симметричность | Если число a является делителем числа b, то число b также является делителем числа a. |
| Единица и число | Каждое число имеет делители 1 и само себя. |
| Строгое включение | Если число a является делителем числа b, и b не равно a, то a является строгим делителем числа b. |
| Ограниченное количество делителей | У каждого числа есть конечное количество делителей. |
| Делители и простые числа | Делители числа делятся на две категории: общие делители с другими числами и уникальные делители, которые принадлежат только данному числу. |
Делители используются для решения различных математических задач, таких как нахождение наибольшего общего делителя, определение простоты чисел и факторизация чисел.
Важно учесть, что делители имеют различные свойства и характеристики в зависимости от типов чисел, над которыми производятся операции. Например, в натуральных числах делителями являются только натуральные числа, а в комплексных числах могут существовать комплексные делители.
Кратное число: определение и примеры

Чтобы выяснить, является ли число кратным, необходимо разделить это число на заданный делитель и проверить отсутствие остатка. Если деление проходит без остатка, то число является кратным, в противном случае оно не является кратным.
Примеры кратных чисел:
| Число | Делитель | Кратное |
|---|---|---|
| 15 | 5 | Да |
| 12 | 3 | Да |
| 20 | 7 | Нет |
| 42 | 6 | Да |
| 56 | 8 | Да |
Таким образом, кратные числа очень полезны в математике и широко применяются в различных задачах и решениях.
Как найти делители и кратные числа?

Делитель – это число, на которое заданное число делится без остатка. Другими словами, делитель делится на заданное число без остатка. Чтобы найти все делители числа, нужно проверить, на какие числа данное число делится без остатка.
Получить все делители числа можно с помощью подбора чисел от единицы до самого числа и проверки, делится ли число на это число без остатка. Если это так, то данное число является делителем.
Кратные числа – это числа, которые делятся на заданное число без остатка. Другими словами, число является кратным, если оно делится на заданное число без остатка. Чтобы найти все кратные числа, нужно умножать данный делитель на различные натуральные числа.
Таким образом, делители являются множителями числа, а кратные числа представляют собой результаты умножения делителя на натуральное число.
Зная концепцию делителей и кратных чисел, можно решать различные задачи, связанные с разложением чисел на множители и поиском чисел, кратных заданному числу.
Практическое применение делителей и кратных чисел

Финансы: Зная делители и кратные чисел, мы можем легко рассчитывать проценты, доли и суммы денег. Например, при расчете процентов на вкладе в банке мы используем кратное число суммы вклада.
Торговля: Разделение и умножение чисел полезно для рассчета стоимости товаров или услуг. Предприниматели используют делители и кратные числа для нахождения оптимальной цены или предложения.
Инженерия: Делители и кратные числа широко используются в инженерных расчетах. Например, при проектировании зданий и мостов необходимо учитывать нагрузку и прочность материалов, что требует знания делителей и кратных чисел.
Разработка программного обеспечения: Математика является одним из ключевых аспектов программирования. Разделение и умножение чисел используются для решения сложных задач в области алгоритмов, оптимизации и анализа данных.
Статистика и наука: Во многих областях науки, таких как физика, химия и биология, необходимо проводить эксперименты и анализировать данные. Понимание делителей и кратных чисел помогает различать паттерны и закономерности в данных.
Все эти примеры демонстрируют практические применения делителей и кратных чисел. Понимание этих концепций не только помогает нам решать математические задачи, но и развивает наши навыки в анализе, решении проблем и применении математических концепций в реальной жизни.
Делитель и кратное число: связь и отличия

Делитель - это число, на которое другое число делится без остатка. Другими словами, если число А делится на число В без остатка, то В является делителем числа А. Например, для числа 10 делителями будут 1, 2, 5 и 10.
Кратное число, с другой стороны, является результатом умножения числа на другое число. То есть, число А является кратным числа В, если оно делится на В без остатка. Например, числа 10, 20 и 50 являются кратными числа 5.
Таким образом, разница между делителем и кратным числом заключается в том, что делитель является числом, на которое другое число делится, а кратное число является результатом умножения числа на другое число и делится на него без остатка.
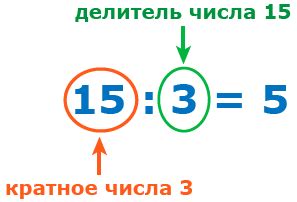
Связь между делителями и кратными числами заключается в том, что число А является кратным числа В, если В является делителем А. Например, число 15 кратно числу 3, потому что 3 является одним из его делителей.
Таким образом, понимание различий и связей между делителем и кратным числом позволяет лучше понять структуру чисел и использовать эти понятия в решении различных математических задач.



