Частное - это результат деления одного числа на другое. В математике частное является одной из основных операций и позволяет нам определить, сколько раз одно число содержится в другом. Для вычисления частного используется специальный символ деления - знак "/".
Частное можно представить в виде числа, которое получается при делении одного числа (делимого) на другое (делитель). Например, если мы разделим число 12 на число 3, то получим частное 4. Это означает, что число 3 содержится в числе 12 четыре раза.
Частное может быть как целым числом, так и десятичной дробью. Если при делении число делится без остатка, то получаем целое число в качестве частного. Например, если мы разделим число 10 на число 2, то получим частное 5. Если же при делении получается остаток, то частное будет представлено в виде десятичной дроби.
Примеры частного при делении:
1. Делимое: 24, Делитель: 6. Частное: 4. В данном примере число 6 содержится в числе 24 ровно 4 раза без остатка.
2. Делимое: 15, Делитель: 4. Частное: 3.75. В данном примере число 4 содержится в числе 15 три раза с остатком 3.75.
3. Делимое: 50, Делитель: 7. Частное: 7.142857142857143. В данном примере число 7 содержится в числе 50 с остатком 7.142857142857143.
Таким образом, частное при делении помогает нам определить, сколько раз одно число содержится в другом и является важным понятием в математике.
Что такое частное?

Например, если мы разделим число 10 на число 2, результатом будет частное равное 5. Это означает, что число 5 вмещается в число 10 ровно два раза.
Частное также может быть меньше, чем делимое. Например, если мы разделим число 5 на число 10, результатом будет частное равное 0,5. Это означает, что число 0,5 вмещается в число 5 ровно один раз, а остается половина от делителя.
Частное играет важную роль в различных математических операциях, таких как вычисление среднего значения, решение уравнений и анализ данных. Оно помогает нам понять отношение между двумя числами и измерить количество одного числа, которое можно получить из другого.
Определение частного в математике

Например, если мы разделим число 10 на число 2, то получим частное равное 5. Это значит, что число 2 содержится в числе 10 пять раз. В другом случае, если мы разделим число 15 на число 3, то получим частное равное 5. Это означает, что число 3 содержится в числе 15 пять раз.
Значение частного в разных областях математики

Понятие частного применяется в различных областях математики и имеет разные значения в каждой из них. Рассмотрим несколько примеров.
1. Арифметика
В арифметике частным называется результат деления одного числа на другое. Например, если разделить число 10 на число 2, получим частное равное 5. Данное понятие частного широко используется в повседневной жизни, например, при расчете скидок, долей и долгов.
2. Алгебра
В алгебре частное является одной из операций, которую можно выполнить над алгебраическими выражениями. Например, при делении двух многочленов получается новый многочлен, являющийся частным от деления. Частное в этом случае может быть как числом, так и многочленом.
3. Теория вероятностей
В теории вероятностей частное представляет собой отношение вероятностей двух событий. Например, частное двух вероятностей может показывать, во сколько раз одно событие более вероятно по сравнению с другим событием.
4. Дифференциальное исчисление
В дифференциальном исчислении частное играет важную роль при нахождении производной функции. Производная функции является частным предела приращения функции и приращения независимой переменной. Частное в этом случае выражает скорость изменения функции по сравнению с изменением независимой переменной.
Таким образом, значение частного в математике зависит от области, в которой оно применяется, и имеет свои особенности в каждой из них.
Примеры частного при делении

Чтобы лучше понять, что такое частное при делении, рассмотрим несколько конкретных примеров:
Делимое: 15
Делитель: 3
Частное: 5
Остаток: 0
В этом примере число 15 делится на число 3 без остатка. В результате получается частное равное 5.
Делимое: 25
Делитель: 7
Частное: 3
Остаток: 4
В этом случае число 25 делится на число 7. В результате получается частное равное 3, а остаток равен 4.
Делимое: 38
Делитель: 5
Частное: 7
Остаток: 3
В этом примере число 38 делится на число 5. Частное равно 7, а остаток равен 3.
Таким образом, частное при делении - это результат деления одного числа на другое. Оно может быть как целым числом, так и десятичной дробью. Остаток от деления также может быть равен нулю или быть положительным числом.
Пример частного при делении двух чисел

Для лучшего понимания концепции частного при делении, рассмотрим следующий пример:
Дано: Делитель - число, на которое будет осуществляться деление. Делимое - число, которое будет делиться.
Пусть у нас есть делитель 4 и делимое 12. Чтобы найти частное, мы делим 12 на 4.
Процесс деления выглядит следующим образом:
12 ÷ 4 = 3
В данном случае, число 12 является делимым, число 4 - делителем, а число 3 - частным.
Это означает, что при делении 12 на 4, получаем частное, равное 3.
Таким образом, в этом примере частное при делении двух чисел равно 3.
Пример частного при делении многочлена на многочлен
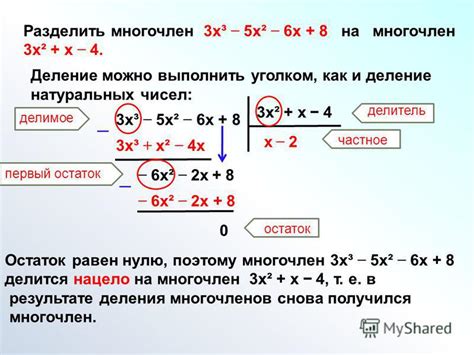
Представим у нас есть два многочлена: делимое и делитель. Для наглядности используем следующий пример:
| Делимое: | x^3 + 4x^2 + 9x - 3 |
| Делитель: | x + 2 |
Чтобы найти частное при делении многочлена на многочлен, следуем стандартному алгоритму деления столбиком:
| x^2 | 2x | 1 | 6 | |
| x + 2 | x^3 | 4x^2 | 9x | -3 |
| - (x^3 + 2x^2) | ||||
| 2x^2 | 9x | -3 | ||
| - (2x^2 + 4x) | ||||
| 5x | -3 | |||
| - (5x + 10) | ||||
| - 13 |
Таким образом, частным при делении многочлена x^3 + 4x^2 + 9x - 3 на многочлен x + 2 будет многочлен x^2 + 2x + 1 с остатком -13.



