Параллелограмм – одна из основных фигур геометрии, и его свойства широко используются в решении задач и построении различных конструкций. В данной статье мы рассмотрим доказательство параллелограмма по данным рисунка.
Для начала, рассмотрим рисунок с изображением фигуры. Эта фигура состоит из четырех отрезков, которые соединяются в вершинах. Наша задача – доказать, что эта фигура является параллелограммом.
Для доказательства параллелограмма, нам необходимо проверить выполнение двух условий: противоположные стороны фигуры должны быть равны и параллельны. Для этого, мы проведем несколько шагов и последовательных доказательств.
В начале, рассмотрим две противоположные стороны фигуры. По условию, эти стороны изображены на рисунке и обозначены. Для простоты, назовем их AB и CD. Составим отрезки AC и BD, которые соединяют концы противоположных сторон.
Рисунок параллелограмма: основная информация
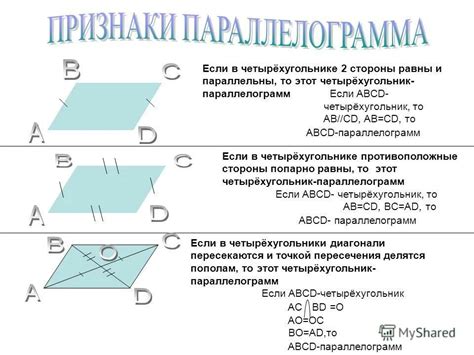
Данная статья предоставляет основную информацию о рисунке параллелограмма. Ниже приведены основные пункты, которые следует учесть при изучении данного рисунка:
- Параллелограмм - это квадрилатерал, у которого противоположные стороны параллельны.
- На рисунке параллелограмма обозначены четыре стороны: AB, BC, CD, DA.
- Противоположные стороны параллелограмма равны по длине.
- Противоположные углы параллелограмма равны по мере.
- На рисунке также видно, что диагонали параллелограмма пересекаются в точке E.
- Диагонали параллелограмма делятся точкой пересечения E пополам.
Рисунок параллелограмма может быть использован для доказательства различных свойств и теорем, связанных с параллелограммами. При изучении данного рисунка важно учесть все вышеперечисленные особенности и свойства параллелограмма.
Параллелограмм: определение и свойства
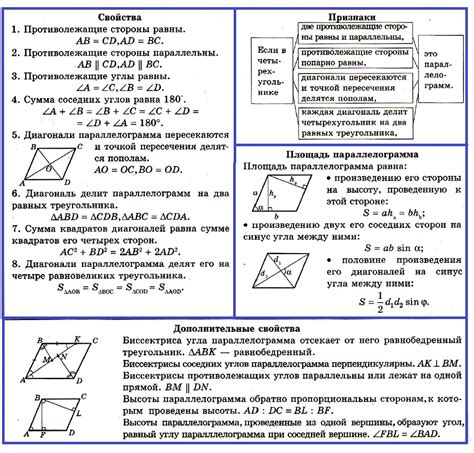
Свойства параллелограмма позволяют нам проводить ряд доказательств и применять их в геометрических задачах. Вот основные свойства параллелограмма:
- Противоположные стороны равны: Две стороны параллелограмма, расположенные друг напротив друга, имеют равные длины.
- Противоположные стороны параллельны: Две стороны параллелограмма, расположенные друг напротив друга, параллельны друг другу.
- Противоположные углы равны: Углы противоположные равных сторон параллелограмма имеют равные значения.
- Диагонали делятся пополам: Диагонали параллелограмма делятся пополам и пересекаются в центре параллелограмма.
- Сумма углов параллелограмма: Сумма углов параллелограмма равна 360 градусам.
Используя эти свойства, мы можем доказывать различные теоремы о параллелограммах и решать задачи, связанные с их конструкциями и свойствами.
Доказательство параллелограмма по данным рисунка
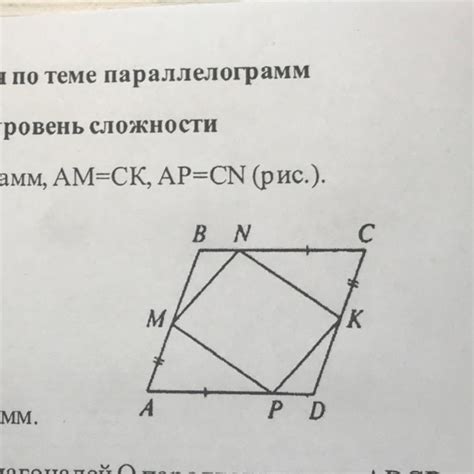
Рассмотрим рисунок исходной фигуры. На нем видно, что стороны AB и CD параллельны и имеют равные длины. Следовательно, выполняется одно из условий параллелограмма.
Также на рисунке видно, что стороны AD и BC параллельны и имеют равные длины. Это еще одно условие параллелограмма.
Таким образом, все четыре стороны параллелограмма параллельны и равны, а значит, по данным рисунка, доказано, что исходная фигура является параллелограммом.
Для аналитического доказательства можно использовать координаты вершин фигуры и показать, что соответствующие векторы, образованные этими вершинами, имеют одинаковые направления и длины.
| Свойства | Доказательство |
|---|---|
| Противоположные стороны параллельны | Условие выполняется, так как стороны AB и CD параллельны |
| Противоположные стороны равны | Условие выполняется, так как стороны AB и CD имеют равные длины |
| Диагонали взаимно делятся пополам | Условие не указано на рисунке, поэтому нельзя доказать |
| Углы при основании равны | Условие не указано на рисунке, поэтому нельзя доказать |
Конструкция параллелограмма
Для построения параллелограмма по данным рисунка имеется несколько способов. Один из них – метод с использованием треугольника.
1. Начнем с построения треугольника ABC, в котором известна длина отрезка AB и угол BAC.
2. Из точки B проведем прямую, параллельную прямой AC.
3. Из точек A и C проведем радиусы этих дуг, которые пересекут прямую, проведенную из точки B. Обозначим эти точки пересечения как D и E.
4. Теперь соединим точки D и E полученными отрезками, чтобы получить стороны параллелограмма.
Таким образом, используя данный метод, мы можем построить параллелограмм по заданным условиям и доказать, что противоположные его стороны параллельны.
Теорема о соответствующих углах параллелограмма

Формально, теорема гласит следующее:
| Если | ABCD | является параллелограммом, |
| то | ∠A = ∠C | (угол A равен углу C) |
| и | ∠B = ∠D | (угол B равен углу D). |
То есть, если рассмотреть параллелограмм ABCD, то углы A и C окажутся равными, а также углы B и D также будут равными.
Теорема о соответствующих углах параллелограмма является важным инструментом в доказательстве различных свойств и теорем о параллелограммах. Она позволяет устанавливать связь между углами параллелограмма, что упрощает решение задач и делает анализ геометрических фигур более систематическим и логичным.
Основные формулы для расчета параллелограмма
| Формула | Описание |
|---|---|
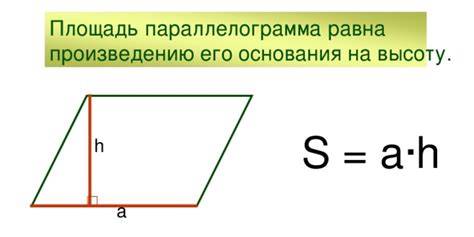
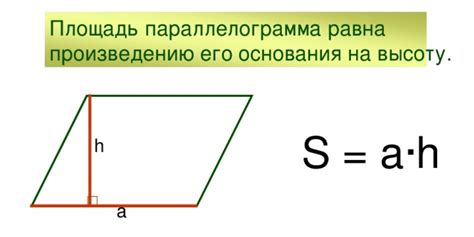
| Площадь | Площадь параллелограмма равна произведению длины основания на высоту, т.е. S = a * h, где a - длина основания, h - высота. |
| Периметр | Периметр параллелограмма равен удвоенной сумме длин его сторон, т.е. P = 2 * (a + b), где a, b - длины сторон. |
| Диагонали | Диагонали параллелограмма делят его на два равных треугольника. Длину диагоналей можно найти с помощью теоремы Пифагора: d = √(a^2 + b^2), где d - длина диагонали. |
| Углы | Углы параллелограмма противолежат равным сторонам и равны между собой. Таким образом, сумма углов параллелограмма равна 360°, а каждый угол равен 180°. |
Используя эти основные формулы, можно решать различные задачи, связанные с параллелограммами, например, находить площадь, периметр, диагонали и углы фигуры.
Параллелограмм и его использование в геометрии

Одно из основных свойств параллелограмма – равенство противоположных сторон. Это означает, что любая линия, проведенная через середину одной стороны параллелограмма, также будет проходить через середину противоположной стороны. Такая линия называется медианой параллелограмма и делит его на два равных треугольника.
Параллелограммы широко используются в геометрии при решении задач на построение и изучение различных свойств геометрических фигур. Они являются основой для построения прямоугольников, ромбов и квадратов.
Параллелограммы также используются для вычисления площади фигур, так как его площадь можно легко выразить через длину одной стороны и высоту, опущенную на эту сторону. Формула площади параллелограмма равна произведению длины основания на высоту.
Кроме того, параллелограммы применяются в физике и инженерии для моделирования различных объектов и конструкций. Например, параллелограммы могут использоваться для моделирования сил, приложенных к твердому телу, а также как базовые элементы в строительстве и архитектуре.
Решение задач на параллелограмм
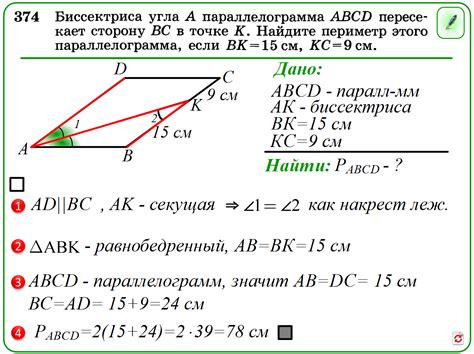
Задачи на параллелограмм часто встречаются в школьном курсе геометрии. Решение таких задач требует знания свойств и формул, связанных с параллелограммами.
Одна из таких задач может быть сформулирована следующим образом: "В параллелограмме ABCD сторона BC равна 6 см, а высота, опущенная на эту сторону, равна 4 см. Найдите площадь параллелограмма."
Для решения данной задачи можно использовать формулу площади параллелограмма: S = a * h, где S - площадь, a - длина стороны параллелограмма, h - высота, опущенная на эту сторону.
В данной задаче известны значения a = 6 см и h = 4 см. Подставляя их в формулу, получим: S = 6 см * 4 см = 24 см².
Таким образом, площадь параллелограмма ABCD равна 24 см².
| Задача | Решение |
|---|---|
| В параллелограмме ABCD сторона AB равна 10 см, а высота, опущенная на эту сторону, равна 8 см. Найдите площадь параллелограмма. | Площадь параллелограмма равна S = a * h = 10 см * 8 см = 80 см². |
| В параллелограмме ABCD сторона AD равна 12 см, а высота, опущенная на эту сторону, равна 5 см. Найдите площадь параллелограмма. | Площадь параллелограмма равна S = a * h = 12 см * 5 см = 60 см². |
Таким образом, решение задач на параллелограмм сводится к использованию формулы площади и подстановке известных значений. Важно помнить свойства параллелограммов и правильно определять, какие значения использовать в формуле.
Параллелограмм: примеры в реальной жизни

Один из простых примеров использования параллелограмма можно найти в строительстве. Когда строители укладывают плитку или керамическую плитку на пол или стену, они часто используют параллелограмм как основу при создании узора. Благодаря параллельным сторонам, плитки располагаются в определенной геометрической форме, создавая эстетически приятный и симметричный дизайн.
Еще один пример применения параллелограмма можно найти в автомобильной промышленности. Параллелограмм используется в подвеске автомобилей для обеспечения плавного движения колес. При сжатии и расширении подвески, параллелограмм сохраняет постоянный угол наклона, что позволяет колесам двигаться вертикально, сохраняя при этом контроль над транспортным средством.
Также параллелограмм находит применение в области архитектуры. Многие строения, такие как мосты или здания, могут иметь прямоугольную или параллелограммическую форму с параллельными сторонами. Это упрощает строительство, расчеты и обеспечивает прочность конструкции.
Не менее важное применение параллелограмма можно найти в компьютерной графике. Графический движок, который создает движение и визуализацию в компьютерных играх, использует параллелограммы для определения и отображения трехмерных объектов. Параллелограммы также используются для текстурирования объектов, добавляя им реалистичные детали и эффекты.
Обратите внимание, что это только несколько примеров применения параллелограмма в реальной жизни. Многие другие области, такие как геодезия, геометрия или дизайн, также находят применение этой формы.



