Алгебра логики – это раздел математики и информатики, изучающий формальное описание и анализ логических выражений и операций. Задачей алгебры логики является разработка методов и инструментов для формализации и решения логических проблем, таких как доказательство истинности логических утверждений, определение логических операций и построение логических схем.
В алгебре логики используются различные символы и операции, такие как конъюнкция (∧), дизъюнкция (∨), отрицание (¬) и импликация (→), которые позволяют формулировать и решать логические задачи. Важным понятием в алгебре логики является понятие истинности логического выражения, которое определяется с помощью таблиц истинности.
Алгебра логики имеет широкое применение в информатике и компьютерных науках. Она является основой для разработки языков программирования, алгоритмического мышления и анализа данных. Алгебра логики помогает строить логические модели реального мира, а также решать проблемы из области искусственного интеллекта и машинного обучения.
Алгебра логики: что это?

Основная цель алгебры логики – разработка методов исследования логических законов и отношений, а также создание формальных систем, которые позволяют анализировать различные аспекты логического мышления.
Алгебра логики широко применяется в информатике, особенно в области дизайна и анализа программных систем. Она позволяет формализовать и структурировать логические выражения и операции, что помогает создавать эффективные и надежные программы.
Основные понятия алгебры логики

В алгебре логики существуют основные понятия, которые являются основой для построения логических выражений:
1. Переменные - символы, которые представляют логические состояния или истинностные значения. Они могут принимать два значения: истина (1) и ложь (0).
2. Логические операции - специальные символы или функции, которые позволяют комбинировать логические значения и получать новые значения. Основные операции включают:
- Конъюнкцию (логическое умножение),
- Дизъюнкцию (логическое сложение),
- Отрицание (логическое отрицание),
- Импликацию (логическое следование).
3. Логические функции - математические функции, которые применяются к логическим значениям. Они определяют, какие значения получают выражения в зависимости от истинности переменных и применяемых операций.
4. Выражения - комбинации переменных, операций и логических функций, которые позволяют выразить логические отношения или утверждения об объектах или событиях.
Алгебра логики широко применяется в информатике для анализа и проектирования логических систем и алгоритмов. Она является основой для построения цифровых схем, программирования и искусственного интеллекта.
Значение алгебры логики в информатике
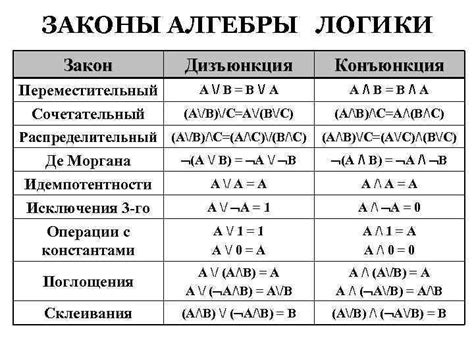
Одно из главных приложений алгебры логики в информатике - это создание и анализ цифровых схем, которые используются в компьютерах и других электронных устройствах. Алгебра логики помогает разработчикам проектировать и оптимизировать логические операции, такие как И, ИЛИ, НЕ, и формулировать их в виде логических уравнений.
Также алгебра логики играет важную роль в разработке программного обеспечения. Она позволяет программистам создавать логические выражения и условные операторы, которые управляют ходом программы и принимают решения на основе логических условий.
Таким образом, алгебра логики является основой для разработки и анализа логических систем и вычислительных моделей. Она позволяет формализовать и оперировать логическими связями и выражениями, что существенно для различных областей информатики и компьютерных наук.
Применение алгебры логики в программировании
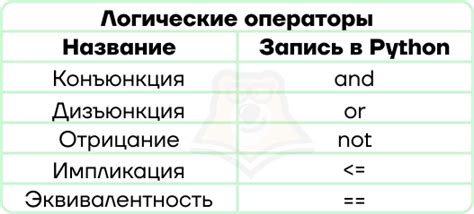
Алгебра логики играет важную роль в программировании, так как она предоставляет набор математических инструментов для работы с логическими значениями и операциями. Вот несколько основных способов, которыми алгебра логики используется в программировании:
Логические выражения: Алгебра логики позволяет создавать логические выражения, которые могут быть использованы для принятия решений в программах. Например, выражение "a > b && b > c" используется для проверки условия, что значение a больше b, а b больше c.
Булевы переменные: Алгебра логики включает в себя работу с булевыми переменными, которые принимают только два возможных значения: истина (true) и ложь (false). Булевы переменные широко используются в программировании для представления логических состояний и управления выполнением кода.
Логические операции: Алгебра логики определяет различные логические операции, такие как "и" (and), "или" (or) и "не" (not), которые могут быть применены к булевым значениям. Эти операции позволяют комбинировать и модифицировать логические выражения и условия.
Логические функции: Алгебра логики также определяет различные логические функции, такие как И, ИЛИ, НЕ и другие, которые могут быть реализованы в виде программных функций или процедур. Эти функции позволяют программистам выполнять сложные операции и преобразования над логическими значениями.
Логические операторы: В языках программирования существуют специальные логические операторы, такие как "if", "else", "while" и другие, которые позволяют использовать алгебру логики для управления выполнением кода в зависимости от логических условий.
Таким образом, алгебра логики является важным инструментом в программировании, который позволяет разрабатывать логические выражения, работать с булевыми переменными и выполнить сложные операции над логическими значениями. Это помогает программистам создавать логичные и эффективные программы.
Алгебра логики и цифровые схемы
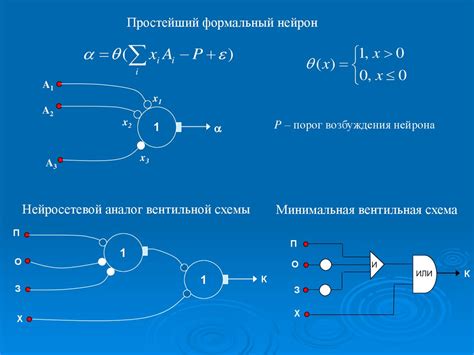
В алгебре логики используются логические операции, такие как И, ИЛИ и НЕ, которые позволяют комбинировать и изменять логические значения, представленные в виде бинарных чисел 0 и 1. Эти операции могут быть представлены в виде логических элементов, таких как вентиль И, вентиль ИЛИ и вентиль НЕ.
Цифровые схемы, построенные на основе алгебры логики, используются во множестве устройств и систем, начиная от простых логических вентилей в компьютерах и микроконтроллерах, и заканчивая сложными процессорами и сетевыми коммутаторами. Они позволяют выполнять цифровую обработку информации, хранить и передавать данные, управлять различными устройствами и многое другое.
Виды логических операций в алгебре логики
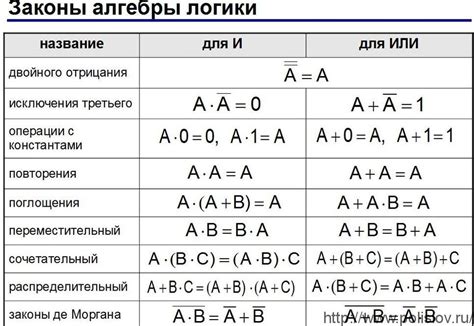
В алгебре логики существует несколько основных видов логических операций, которые широко используются в различных областях информатики:
1. Конъюнкция (логическое И) - это операция, результат которой истинен, если все входные значения также являются истинными. Операция обозначается символом "∧".
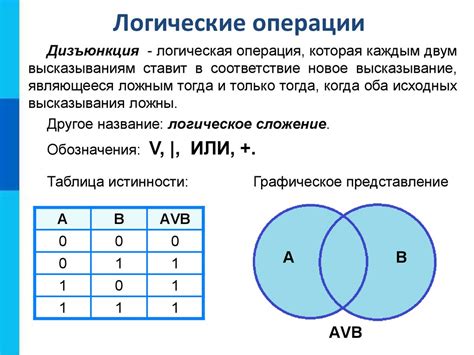
2. Дизъюнкция (логическое ИЛИ) - это операция, результат которой истинен, если хотя бы одно из входных значений истинно. Операция обозначается символом "∨".
3. Отрицание (логическое НЕ) - это операция, результат которой является отрицанием входного значения. Если входное значение истинно, результат будет ложным, и наоборот. Операция обозначается символом "¬".
4. Импликация (логическое СЛЕДУЕТ) - это операция, результат которой истинен, если из первого входного значения следует второе входное значение. Операция обозначается символом "→".
5. Эквиваленция (логическое, ЕСЛИ И ТОЛЬКО ЕСЛИ) - это операция, результат которой истинен, если оба входных значения равны. Операция обозначается символом "↔".
Эти логические операции предоставляют мощные инструменты для анализа и работы с логическими выражениями. Применение алгебры логики в информатике позволяет решать сложные задачи и создавать эффективные алгоритмы для обработки информации.
Алгебра логики и математические логики
Алгебра логики предоставляет набор методов и правил для работы с логическими операциями, такими как «И», «ИЛИ» и «НЕ», а также для построения и анализа логических выражений и утверждений. Она является основой для многих других важных областей информатики, включая цифровую логику, компьютерные алгоритмы и искусственный интеллект.
Математические логики изучают исчисление и формализацию логических систем с использованием математических методов. Они стремятся разработать строгое математическое описание различных систем логического рассуждения и доказательства и вывести логические законы и правила на основе математических оснований. Математические логики также изучают связь между логикой и другими областями математики, такими как алгебра, теория множеств и теория вычислимости.
Алгебра логики и математические логики играют важную роль в информатике, помогая разработчикам и исследователям разрабатывать и анализировать сложные логические системы, создавать эффективные алгоритмы и доказывать корректность программ. Знание алгебры логики и математических логик является необходимым для понимания и применения многих концепций и методов в информатике и связанных областях.
Важность изучения алгебры логики для разработчиков

Основное преимущество изучения алгебры логики для разработчиков заключается в возможности улучшить логическое мышление и способность анализировать сложные задачи. Разработчики, знакомые с основами алгебры логики, способны детально исследовать и понимать логику работы программ и алгоритмов.
Знание алгебры логики также помогает разработчикам создать эффективные и надежные программы. Она помогает выявлять и исправлять ошибки и несоответствия в программном коде, а также оптимизировать работу программы путем улучшения логической структуры и алгоритмов.
Исключительно важно понимать, что изучение алгебры логики помогает разработчикам строить ясную и структурированную логику программного кода. Это улучшает понимание кода другими разработчиками, упрощает сотрудничество и позволяет избежать недоразумений.
Кроме того, алгебра логики играет значительную роль в изучении других областей информатики, таких как искусственный интеллект, базы данных и криптография. Знание основ алгебры логики позволяет разработчикам глубже понять и применить эти области в своей работе.
В целом, изучение алгебры логики является обязательным элементом для разработчиков, помогая им улучшить свои навыки логического мышления, повысить качество программного кода и успешно работать в различных областях информатики.
История развития алгебры логики

В средние века алгебра логики развивалась в работах философов и логиков, таких как Джордано Бруно и Готфрид Лейбниц. Они внесли важные вклады в теорию логических высказываний и математическую логику.
Однако настоящий прорыв в алгебре логики произошел в 19-20 веках. Логика была формализована и стала математической дисциплиной. Основные понятия и определения были разработаны Жоржем Булем и Георгом Кантором, которые создали алгебры Буля и множественной логики.
Сегодня алгебра логики активно применяется во многих областях информатики, таких как компьютерные науки, искусственный интеллект, теория баз данных и другие. Она является ключевым инструментом для разработки и анализа сложных вычислительных систем.



