Алгебраическая дробь - это математический объект, который представляет собой отношение двух многочленов. В 8 классе алгебраическая дробь становится одним из ключевых понятий, с которым ученикам необходимо ознакомиться. Понимание основных понятий алгебраической дроби является основой для дальнейшего изучения алгебры и решения сложных задач.
Одно из главных понятий алгебраической дроби - это разложение на простейшие дроби. Разложение на простейшие дроби позволяет представить сложную алгебраическую дробь в виде суммы простых дробей. Для этого необходимо найти все корни знаменателя и записать разложение на простые дроби в виде суммы их частей, умноженных на множители-степени соответствующих корней.
Ещё одним важным понятием алгебраической дроби является операция умножения. При умножении алгебраических дробей необходимо умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби. После этого полученные произведения сокращаются до простейшего вида, если это возможно.
Основные понятия в алгебре
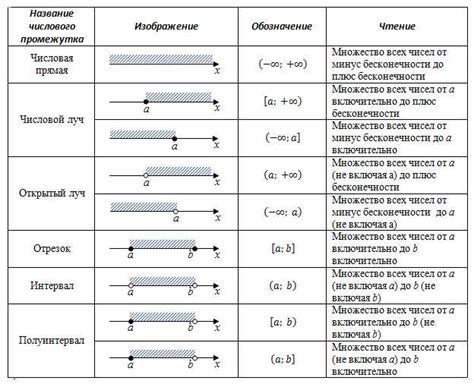
Одно из основных понятий в алгебре - это алгебраическая дробь. Алгебраическая дробь представляет собой отношение двух алгебраических выражений. Она состоит из числителя и знаменателя, которые могут содержать переменные и арифметические операции.
Другим важным понятием в алгебре является уравнение. Уравнение - это математическое выражение, в котором неизвестная величина связана с другими известными величинами с помощью знаков равенства или неравенства. Решение уравнения - это такая неизвестная величина, при подстановке которой равенство выполняется.
Для решения уравнений используются различные методы и приемы, такие как подстановка, факторизация, разложение на множители и т.д. Важно уметь анализировать уравнение и применять соответствующие методы для его решения.
Еще одним понятием в алгебре является функция. Функция - это математическое соответствие между двумя множествами, при котором каждому элементу одного множества соответствует ровно один элемент другого множества. Функции широко используются во всех областях математики и имеют множество приложений в реальной жизни.
Другие важные понятия в алгебре включают операции над числами, системы уравнений, графики функций, матрицы и т.д. Освоение основных понятий в алгебре позволяет лучше понимать и решать различные математические задачи, а также найти их применение в реальной жизни.
Что такое алгебраическая дробь?

Числитель и знаменатель могут быть представлены как многочлены, которые включают переменные и коэффициенты. Например, алгебраическая дробь может иметь вид (3x^2 + 2x + 1)/(x - 4). В этом примере, числитель - многочлен 3x^2 + 2x + 1, а знаменатель - многочлен x - 4.
Одна из основных операций с алгебраическими дробями - это их упрощение. Упрощение алгебраической дроби заключается в нахождении общего делителя числителя и знаменателя и сокращении дроби до наименьших значений. Например, дробь (6x^2 + 3x)/(2x) можно упростить до 3x + 1.
Алгебраические дроби также могут быть сложены, вычтены, умножены и разделены между собой. При выполнении этих операций необходимо учитывать правила работы с многочленами и выполнение необходимых алгебраических операций.
Знание основных понятий алгебраической дроби и умение выполнять операции с ними являются важными навыками в алгебре и могут быть применены в различных областях, включая алгебраическое моделирование, физику и экономику.
Примеры алгебраических дробей:

В алгебре алгебраической дробью называется дробь, в которой числитель и знаменатель могут быть полиномами. Рассмотрим несколько примеров алгебраических дробей:
Пример 1:
Дана алгебраическая дробь: 2x2 - 6x + 4/3x - 9.
Числитель данной дроби представляет собой полином второй степени, а знаменатель - полином первой степени. Сокращать данную дробь нельзя, так как никакой общей части у числителя и знаменателя нет. Дробь можно упростить, выполнив деление каждого слагаемого числителя на 2 и каждого слагаемого знаменателя на 3. Получим упрощенную алгебраическую дробь: 1x2 - 3x + 2/1x - 3.
Пример 2:
Дана алгебраическая дробь: x3 - x/x + 1.
В данном случае числитель представляет собой полином третьей степени, а знаменатель - полином первой степени. Дробь нельзя сократить, так как общей части у числителя и знаменателя нет. Упрощение данной дроби не требуется.
Пример 3:
Дана алгебраическая дробь: 2a2 - 8ab + 7/3a2 + 9ab.
Числитель данной дроби представляет собой полином второй степени, а знаменатель - полином второй степени. В данном случае дробь можно сократить, так как числитель и знаменатель имеют общий множитель 2a. После сокращения получим упрощенную алгебраическую дробь: 1a - 4b + 7/3a + 3b.
Приведенные примеры помогут вам лучше понять, какие могут быть алгебраические дроби и как их упрощать или сокращать.
Операции с алгебраическими дробями

Операции с алгебраическими дробями включают сложение, вычитание, умножение и деление. Давайте рассмотрим каждую операцию подробнее.
Сложение и вычитание алгебраических дробей
Для сложения или вычитания алгебраических дробей необходимо привести дроби к общему знаменателю. Для этого необходимо разложить знаменатели на множители и учесть особенности каждого случая.
Затем складываем или вычитаем числители и записываем результат с общим знаменателем. Не забудьте сократить полученную дробь, если это возможно.
Умножение алгебраических дробей
Умножение алгебраических дробей осуществляется путем перемножения числителей и знаменателей. Затем сокращаем полученную дробь, если это возможно.
Для упрощения умножения можно сократить числитель одной дроби с знаменателем другой дроби, если в числителе и знаменателе содержатся одинаковые множители.
Деление алгебраических дробей
Деление алгебраических дробей сводится к умножению первой дроби на обратную второй дробь. То есть, если у нас есть дроби a(x) / b(x) и c(x) / d(x), то результатом деления будет дробь a(x) / b(x) умноженная на d(x) / c(x).
Важно отметить, что при делении дробей необходимо проверять, делится ли знаменатель второй дроби на знаменатель первой дроби. Если это не выполняется, то результатом деления будет неправильная дробь.
Теперь, учитывая эти операции, вы можете выполнять арифметические действия с алгебраическими дробями и решать задачи, связанные с этой темой.
Упрощение алгебраических дробей
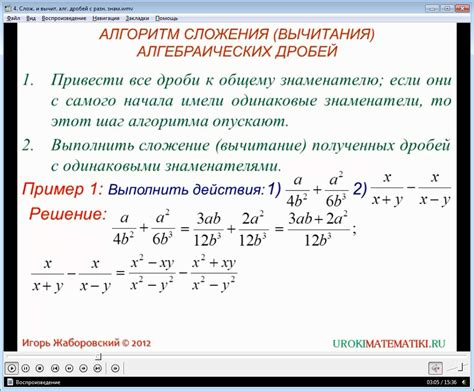
Для упрощения алгебраической дроби можно использовать следующие методы:
1. Факторизация числителя и знаменателя.
Первым шагом необходимо разложить числитель и знаменатель на простые множители. Используя свойства алгебры, можно вынести общие множители и сократить дробь.
2. Представление дроби в виде суммы нескольких дробей.
Если у дроби есть многочлен в знаменателе, то можно представить дробь в виде суммы нескольких простых дробей. Для этого необходимо разложить многочлен на множители и применить метод частных дробей.
3. Сокращение общих множителей.
Если в числителе и знаменателе дроби есть общие множители, они могут быть сокращены. Для этого нужно найти наибольший общий делитель числителя и знаменателя и поделить их на него.
Упрощение алгебраических дробей позволяет упростить вычисления и решение уравнений, содержащих дроби. Знание методов упрощения дробей является важным навыком при изучении алгебры и других математических дисциплин.
Применение алгебраических дробей в решении уравнений

Один из способов применения алгебраических дробей в решении уравнений – это нахождение общего знаменателя для всех дробей в уравнении. Общий знаменатель нужен для упрощения выражений и получения более простых уравнений.
Для нахождения общего знаменателя мы можем воспользоваться методом наименьших общих кратных (НОК) знаменателей всех дробей. Затем мы приводим каждую дробь к общему знаменателю и складываем их числители. Полученное выражение равно нулю, что позволяет нам решить уравнение.
Применение алгебраических дробей также помогает нам в решении уравнений с одной неизвестной, в которых дроби являются переменными. Мы можем записать такое уравнение в виде алгебраической дроби и привести его к общему знаменателю. Затем мы сравниваем числитель и знаменатель, чтобы определить значения переменной.
Важно отметить, что при применении алгебраических дробей в решении уравнений, необходимо учитывать возможность появления дополнительных решений или исключений. При делении на нуль или при наличии неправильных алгебраических дробей возникают дополнительные условия и ограничения, которые нужно учитывать при решении уравнений.
| Преимущества применения алгебраических дробей в решении уравнений: |
|---|
| - Упрощение комплексных выражений и уравнений |
| - Возможность анализировать и понимать структуру уравнений |
| - Решение уравнений с переменными в знаменателе |
| - Решение уравнений с переменными в числителе и знаменателе |
| - Упрощение вычислений и сокращение времени решения уравнений |



