Квадратный корень из числа - это такое число, которое возводя в квадрат, даёт исходное число. Когда мы говорим о корнях из числа, то чаще всего имеем в виду положительный квадратный корень.
Корень квадратный обозначается символом √. Например, корень квадратный из 4 обозначается как √4 = 2. Однако, кроме положительного, для каждого положительного числа существует и отрицательный квадратный корень. Например, корень квадратный из 4 может быть и -2.
Как же найти квадратный корень из числа? Существует специальная формула - формула корня квадратного, которая позволяет найти значение корня квадратного из числа. Формула имеет вид: корень квадратный из числа a равен квадратному корню из a, то есть √a.
Формула для нахождения квадратного корня числа 2

Квадратный корень из числа 2 можно найти с помощью специальной формулы. Для этого применяется формула: .
Данная формула означает, что нужно найти число, которое, возведенное в квадрат, равно 2. Квадратный корень - это число, при возведении в квадрат которого получается исходное число.
Используя данную формулу, можно рассчитать значение квадратного корня из числа 2: .
Таким образом, квадратный корень из числа 2 приближенно равен 1.414. Это значение является иррациональным числом, то есть его десятичная часть не повторяется и не прекращается.
Что такое квадратный корень и зачем он нужен?

Основное предназначение квадратного корня – нахождение и извлечение корней из числовых выражений. Он позволяет найти число, которое при возведении в квадрат дает исходное значение. Квадратный корень также применяется в различных областях науки и техники, таких как физика, инженерия и статистика.
Квадратный корень может быть использован для нахождения длины стороны квадрата, если известна его площадь, или для определения длины стороны треугольника, если известны площадь и гипотенуза. Он также помогает решать уравнения с квадратными корнями и находить среднее арифметическое.
Извлечение квадратного корня осуществляется с помощью специальных математических функций, а также с помощью калькуляторов или компьютерных программ. На практике квадратный корень может быть выражен в виде десятичной дроби или в виде иррационального числа.
Изучение квадратного корня и его свойств помогает в понимании основных математических операций и развитии логического мышление. Знание данной математической операции полезно не только для решения задач, но и в повседневной жизни, например, при расчете площади квадратных или прямоугольных поверхностей, определении длины стороны геометрических фигур и других ситуациях, где требуется нахождение квадратных корней.
Основные свойства квадратного корня

Основные свойства квадратного корня следующие:
| Свойство | Описание |
| 1. Существование | Квадратный корень из неотрицательного числа всегда существует. |
| 2. Уникальность | Квадратный корень из числа определен однозначно, и для положительных чисел он всегда положителен. |
| 3. Возведение в квадрат | Квадратный корень из числа и его возведение в квадрат взаимообратные операции. |
| 4. Арифметические операции | Квадратный корень обладает свойством аддитивной и мультипликативной согласованности, то есть сумму (или произведение) корней можно вычислить как корень из суммы (или произведения) соответствующих чисел. |
| 5. Дистрибутивность | Квадратный корень является дистрибутивным относительно операций сложения и вычитания. |
Использование этих свойств помогает упростить вычисления и решение задач, связанных с квадратными корнями.
Как находить квадратный корень числа 2?

Одним из способов нахождения приближенного значения квадратного корня из 2 является применение формулы Ньютона-Рафсона. Эта формула позволяет находить более точные приближения квадратного корня путем итеративных вычислений.
Для получения приближенного значения квадратного корня из 2 с помощью формулы Ньютона-Рафсона можно использовать следующие шаги:
1. Задать начальное приближение. Можно выбрать любое число, например, 1.
2. Вычислить новое приближение по формуле: xn+1 = (xn + 2/xn)/2, где xn – текущее приближение.
3. Повторять шаг 2 до достижения желаемой точности. Чем больше итераций, тем более точное приближение будет получено.
Например, при первой итерации начальное приближение 1 дает следующее приближенное значение: x1 = (1 + 2/1)/2 = 3/2 = 1.5.
Далее, повторными итерациями можно приблизиться к искомому значению квадратного корня из 2 с большей точностью.
Значение квадратного корня из 2 можно также найти с помощью калькулятора или специальных математических программ, которые предоставляют точные значения иррациональных чисел.
Примеры использования формулы и расчеты

Формула для вычисления квадратного корня из числа 2 довольно проста:
√2 = 1.414213...
Ниже приведены значения квадратного корня из числа 2, округленные до 6 десятичных знаков:
| Значение | Округленный результат |
|---|---|
| √2 | 1.414213 |
| √2 + √2 | 2.828427 |
| 2√2 | 2.828427 |
| √2 * √2 | 2 |
| √22 | 2 |
Формула для квадратного корня из числа 2 может использоваться в различных математических и физических расчетах. Например, при решении задач по геометрии, при моделировании физических процессов или при анализе статистических данных.
Одним из примеров использования формулы является расчет гипотенузы прямоугольного треугольника, если известны длины его катетов:
Пусть a = 3 и b = 4, тогда применяя формулу a2 + b2 = c2, получаем:
32 + 42 = c2
9 + 16 = c2
25 = c2
c = √25 = 5
Таким образом, с применением формулы для квадратного корня, мы можем вычислить значение гипотенузы треугольника.
Приложение: таблица квадратных корней
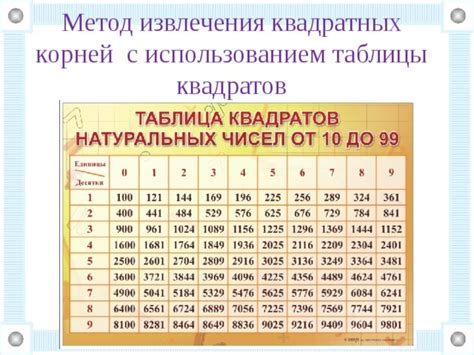
Чтобы упростить процесс нахождения квадратных корней, можно использовать таблицу, в которой представлены значения корней для различных чисел. Такая таблица может быть полезна как для школьников, изучающих математику, так и для всех желающих быстро найти квадратный корень.
В таблице представлены квадратные корни для чисел от 0 до 100 с точностью до двух знаков после запятой. Значения корней вычислены заранее и заключены в таблицу для удобства использования.
Пример таблицы квадратных корней:
| Число | Квадратный корень |
|---|---|
| 0 | 0.00 |
| 1 | 1.00 |
| 2 | 1.41 |
| 3 | 1.73 |
| 4 | 2.00 |
| ... | ... |
Такая таблица позволяет быстро определить квадратный корень для нужного числа без необходимости проводить вычисления самостоятельно. Для получения более точных значений можно использовать специализированные программы или калькуляторы.
Использование таблицы квадратных корней может значительно упростить решение задач, связанных с нахождением квадратного корня. Она предоставляет готовые значения, которые можно применить в тех ситуациях, где точность не играет решающей роли или где нет возможности проводить вычисления вручную.
Таким образом, таблица квадратных корней является полезным инструментом, который помогает быстро найти значения корней и упростить математические вычисления.
В данной статье мы рассмотрели формулу для нахождения квадратного корня из числа 2. Она представляет собой математическую операцию, при которой мы находим число, которое при возведении в квадрат равно 2. Эта формула называется "Формула квадратного корня из 2".
Мы также узнали, что квадратный корень из 2 – это иррациональное число, то есть оно не может быть представлено в виде десятичной дроби или обыкновенной дроби. Его численное значение приближенно равно 1.41421356.
Открытие формулы для нахождения квадратного корня из 2 было важным шагом в развитии математики и имеет множество применений в научных и инженерных расчетах. Знание этой формулы может быть полезным при решении различных задач и заданий в области математики и физики.



